
Therefore, an algebraic sign (+ or ) must be included with each one to denote direction. The variables y, a y, v y, and v 0 y are scalar components. With these data, Equation 3.5b ( ) can be used to find the fall time. The acceleration is that due to gravity, so a y = ≩.80 m/s 2. Furthermore, when the package hits the ground, the y component of its displacement is y = ≡050 m, as the drawing shows. We note that the package is moving initially in the horizontal or x direction, not in the y direction, so that v 0 y = 0 m/s. Therefore, we can focus solely on the vertical part. In falling, it moves to the right, as well as downward, but these two parts of the motion occur independently. The time required for the package to hit the ground is the time it takes for the package to fall through a vertical distance of 1050 m. The package falling from the plane is an example of projectile motion, as Examples 2 and 3 discuss. Ignoring air resistance, determine the time required for the package to hit the ground. The plane releases a “care package” that falls to the ground along a curved trajectory.
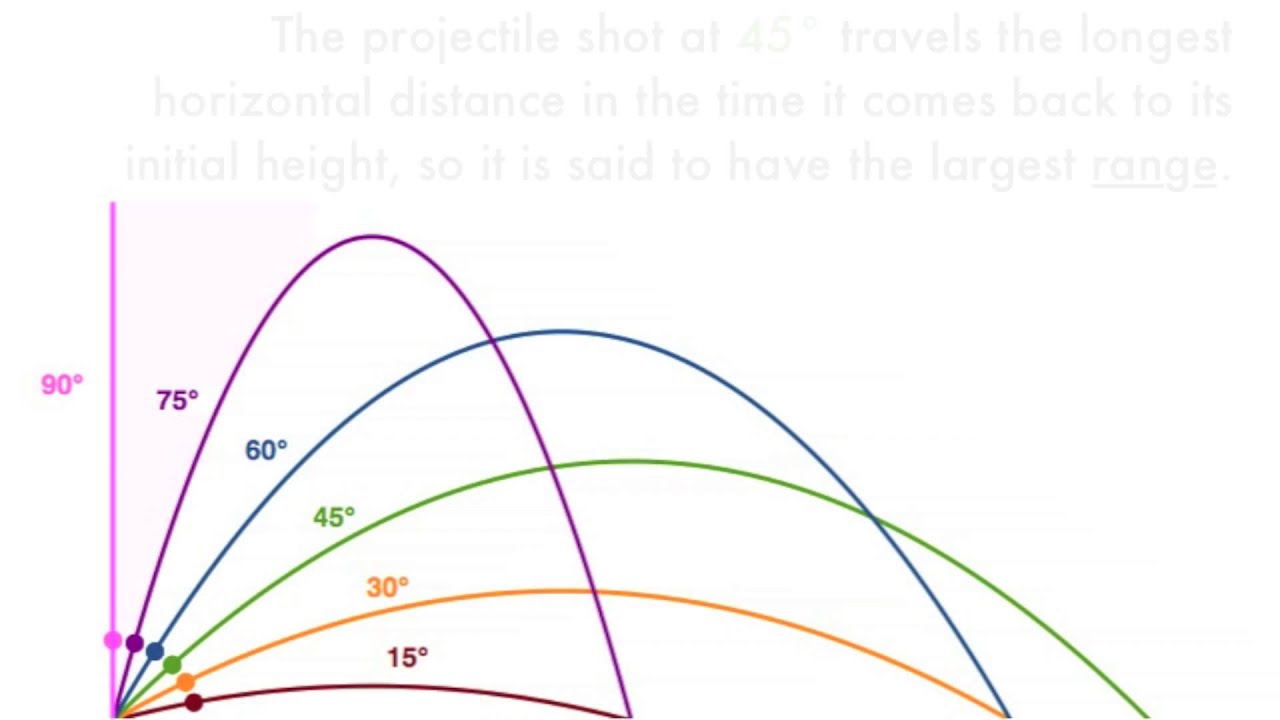
The directions to the right and upward have been chosen as the positive directions. (© Stephen Dalton/Photo Researchers).įigure 3.9 shows an airplane moving horizontally with a constant velocity of +115 m/s at an altitude of 1050 m. In this time-lapse photograph, the cat exhibits projectile motion while in the air, assuming that the effects of air resistance can be ignored. Example 2 and other examples in this section illustrate how the equations of kinematics are applied to projectile motion.įigure 3.8 CONCEPTS AT A GLANCEIn projectile motion, the horizontal or x component of the acceleration is zero, and the vertical or y component of the acceleration is the acceleration due to gravity. In this text, then, the phrase “projectile motion” means that a x = 0 m/s 2 and a y equals the acceleration due to gravity, as the Concept-at-a-Glance chart in Figure 3.8 summarizes. If the path or trajectory of the projectile is near the earth’s surface, a y has a magnitude of 9.80 m/s 2. The y component of the acceleration a y is the downward acceleration due to gravity. As a result, the y component of the velocity v y is not constant, but changes.
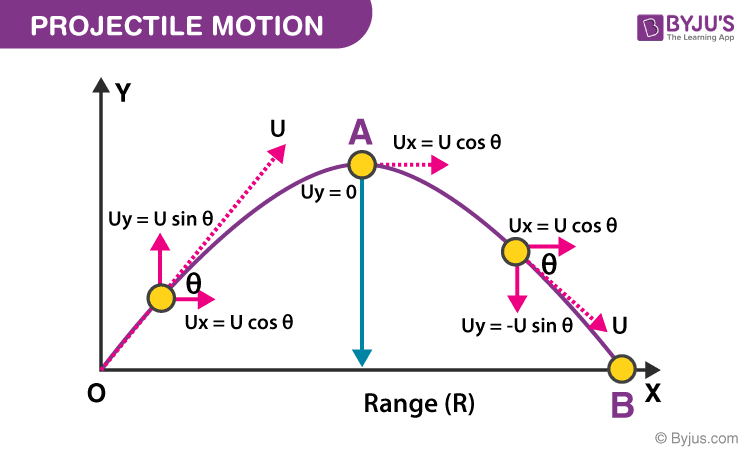
In the vertical or y direction, however, the projectile experiences the effect of gravity. Thus, the x component of the velocity remains constant at its initial value or v x = v 0 x, and the x component of the acceleration is a x = 0 m/s 2. In the horizontal or x direction, the moving object (the projectile) does not slow down in the absence of air resistance. The motion of the ball on its curving path into the stands is a common type of two-dimensional motion called “projectile motion.” A good description of such motion can often be obtained with the assumption that air resistance is absent.ĬONCEPTS AT A GLANCE Following the approach outlined in Figure 3.6, we consider the horizontal and vertical parts of the motion separately.

The biggest thrill in baseball is a home run.


 0 kommentar(er)
0 kommentar(er)
